FLUIDS

( 2021-2022 )

I’ve recently revisited some work on computational fluid dynamics that I started in 2017; this time I'm using new methods that capture more detail in the movements of the fluids. This work is still ongoing. I'm hoping to explore some ideas around fractals and loops via a feedback mechanism. I'm also using these simulations to explore a parallel thread around digital marbling and suminagashi.

The underlying simulation methods used in this work are based on the paper Efficient and Conservative Fluids Using Bidirectional Mapping. I’ve adapted these methods to run in WebGL/glsl and optimized them for realtime performance. I'm hoping to release this simulation code as a javascript library sometime in 2022.

Atmospheric simulation of wispy clouds. This animation was created somewhat unintentionally after running a thin-film simulation for longer than I’d previously done before. Numerical dissipation in the simulation caused the heavier, multicolored components to fade away, leaving behind a monochromatic look with swirling ripples of black, white, and grey. I later colorized this video with tones of blue to give it more of an atmospheric appearance. I'm hoping to explore this thread further.

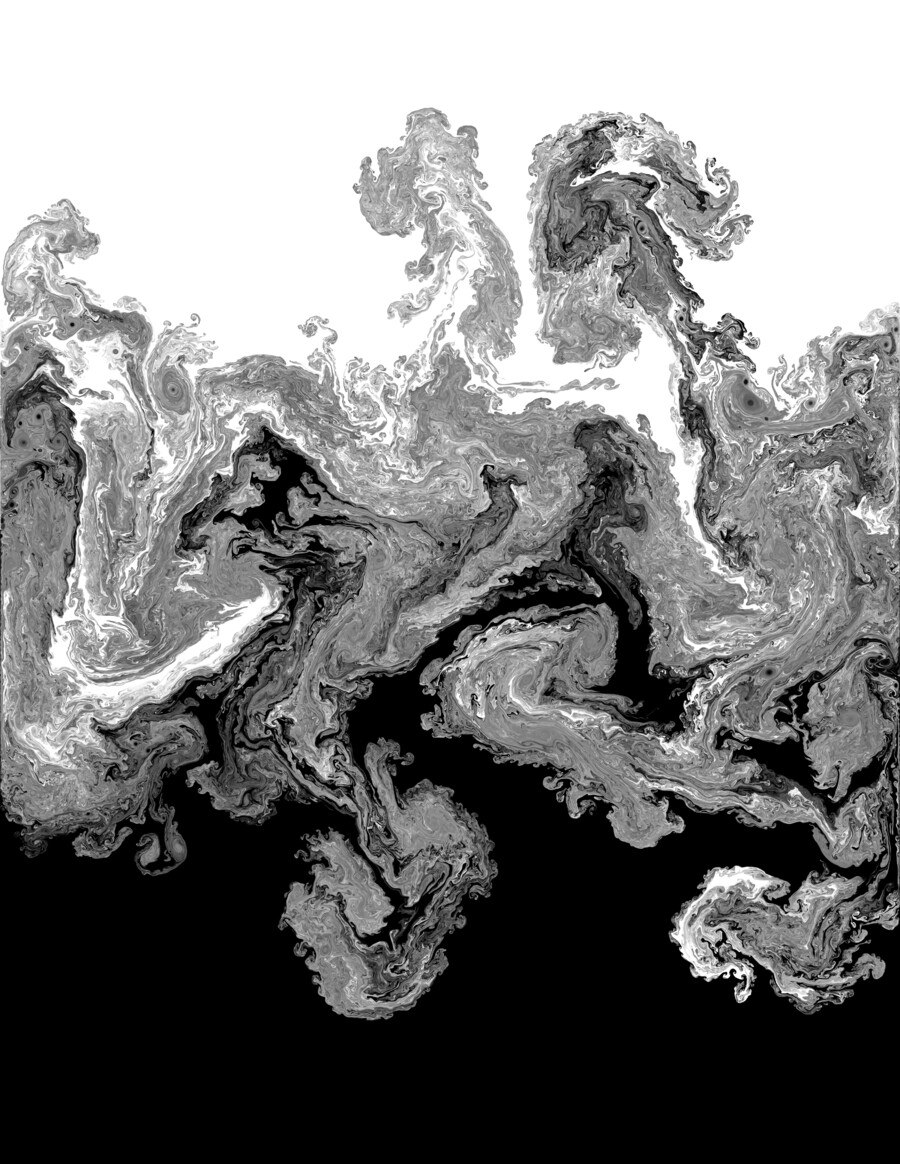
Rayleigh-Taylor Instability: A dense fluid (white) sits on top of a more buoyant fluid (black) with a sinusoidal boundary between them. As the simulation runs under the effect of gravity, "fingers" emerge at the interfaces, eventually causing the fluids to mix. Fractal patterns of vortices can also be observed throughout this process.

Large and small vortices emerging behind an asymmetrical object in the path of the flow. A white ribbon highlights the undulations of the fluid.

An early experiment toward simulating combing patterns in marbled paper. Eight parallel jets comb the fluid downward, and initially form a tidy pattern (there's not enough viscosity in the fluid to call it a laminar flow, but it's somewhat similar). A tiny nudge throws the whole system out of equilibrium and into chaos.

A continual source of inspiration are the bugs that I accidentally introduce into the program along the way. A bug in the code doesn't directly affect the state of the fluid system (i.e. it doesn't look like a smudge of color where it shouldn't be) – instead, these bugs affect the dynamics of the system, yielding surprising new textures and shapes. Oftentimes things become very unstable and interesting results are ephemeral and hard to reproduce.

Vortex street spontaneously forming behind an obstacle. This simulation has some integration issues (as in, problems computing an integral) that cause excess turbulence to emerge in the system.