Fluid Simulation Vortex Shedding Reaction Diffusion Mass Spring Damper Conway
RELATED:
 DIGITAL MARBLING
DIGITAL MARBLING
 FLUIDS
FLUIDS
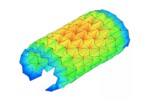
 SHELL FORM FINDING
SHELL FORM FINDING
 ORIGAMI SIMULATOR
ORIGAMI SIMULATOR
 AMOEBA
AMOEBA
Shader programs are executed by the GPU to perform highly parallel computations much more efficiently than possible with a CPU. Currently, WebGL allows GPU programs to read and write to images called “textures”. By encoding input and output data as RGBA pixels in texture images, it’s possible to use the GPU to perform arbitrary calculations in a web browser; this technique is sometimes called “General-Purpose GPU” (GPGPU), since the GPU is not used exclusively for graphics rendering. The following are a collection of programs I’ve written (mostly physics simulations), where math or other logic is processed in WebGL fragment shader programs in order to solve a large system efficiently.
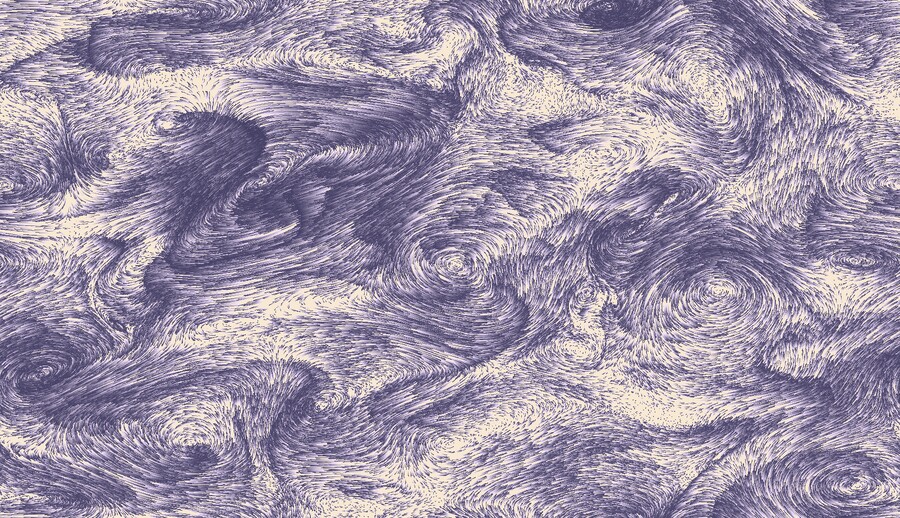
Building off my work on realtime fluid simulations with WebGL, I've been building a physics-based marbling simulation to explore the ways that paper marbling can be augmented through digital tools. I'm interested in exploring new aesthetics using virtual brushes and combs that can only exist in a digital medium.
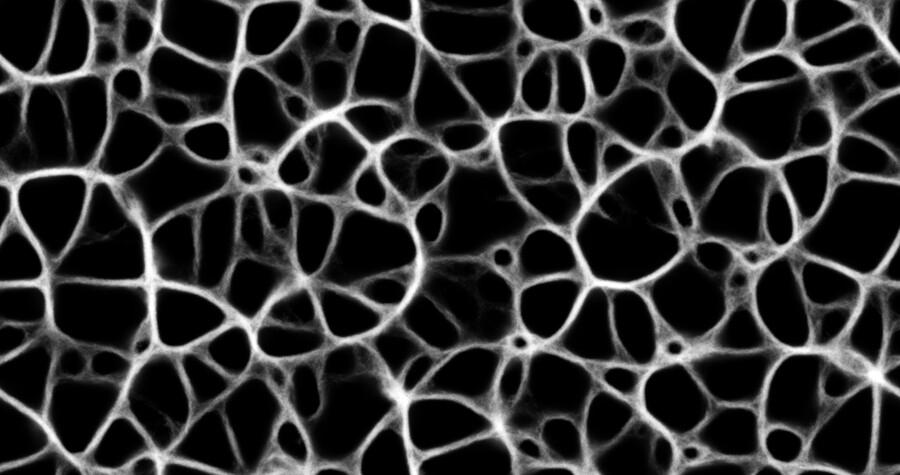
This app simulates the network effects of a multicellular slime mold (Physarum polycephalum), based on a 2010 paper by Jeff Jones: "Characteristics of pattern formation and evolution in approximations of Physarum transport networks" and work by Sage Jenson. In this simulation, simple particle "agents" interact with an underlying field of chemical attractants to form complex, emergent behaviors. Live demo here, code on Github.
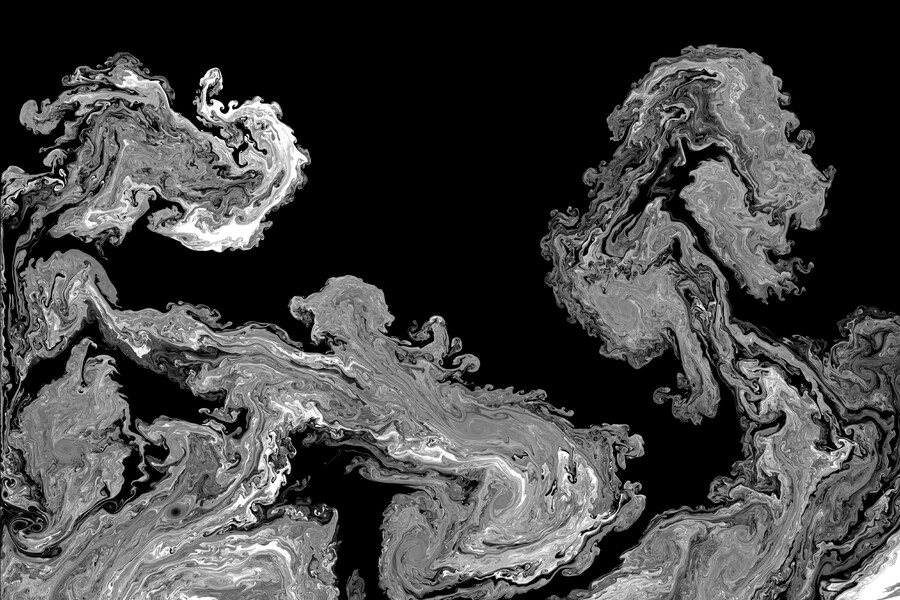
I’ve recently revisited some work on computational fluid dynamics that I started in 2017; this time I'm using new methods that capture more detail in the movements of the fluids. This work is still ongoing. I'm hoping to explore some ideas around fractals and loops via a feedback mechanism. I'm also using these simulations to explore a parallel thread around digital marbling and suminagashi. The underlying simulation methods used in this work are based on the paper Efficient and Conservative Fluids Using Bidirectional Mapping. I’ve adapted these methods to run in WebGL/glsl and optimized them for realtime performance. I'm hoping to release this simulation code as a javascript library sometime in 2022.
This simulation solves the Navier-Stokes equations for incompressible fluids in a GPU fragment shader. Click and drag to apply forces to the fluid and move several thousand Lagrangian particles through the fluid's velocity field. To increase performance, the underlying fluid simulation is solved at a lower resolution and subsampled to smooth out artifacts caused by this speedup. All updates computed on the GPU following methods described in Real-time ink simulation using a grid-particle method. Live demo here, code on Github.

This simulation solves the Navier-Stokes equations for incompressible fluid flow past an obstacle in a GPU fragment shader. It exhibits a phenomenon called vortex shedding, where vortices of alternating spin spontaneously emerge behind the obstacle. Click and drag to interact with the fluid in realtime. To increase performance, I solved for the velocity vector field of the fluid at a lower resolution than I used to compute the distribution of material moving through the fluid (shown in black and white). The Navier Stokes solver was adapted to WebGL from the article Fast Fluid Dynamics Simulation on the GPU. Live demo here, code on Github.
This app simulates a simple reaction-diffusion system, where two virtual chemicals interact to create dynamic patterns. Similar systems were proposed by Alan Turing in 1952 as a mechanism for pattern formation in plants and animals. This reaction-diffusion system is particularly sensitive to two parameters: K (varies along x-axis) and F (varies along y-axis). You can interactively explore regions of K,F parameter space by zooming and panning across the screen. Code on Github, demo available here.
A physics simulation of a mesh of masses attached to their four nearest neighbors with springs and dampers, all running in a GPU fragment shader with WebGL. In the simulation, each pixel on the screen is a mass in a 2D mesh. At each frame, the masses exert forces on each other and the resulting acceleration, velocity, and position of each mass is solved via Euler integration. The vertical displacement of the masses is indicated by the color of the pixel, blue pixels have positive vertical displacement, white have negative displacement, and pink is zero displacement. Scrolling over with your mouse applies an upward force to the nearby pixels. The physics is equivalent to a discrete, damped 2D wave equation or cloth simulation. Masses at the edges of the screen are fixed with zero displacement, making the simulation behave like a giant trampoline. Live demo here, code on Github.
A simple implementation of Conway’s Game of Life in a fragment shader. Use your mouse to add new living cells into the world. Change the birth and survival rules in the menu to control the dynamics of the system. Code on Github, demo available here.